
Jul 21, 2022 \ Finance
Man GroupがGraphcore IPUを使用した超並列オプション価格設定を切り拓く
筆者
Luke Markham

Jul 21, 2022 \ Finance
筆者
Luke Markham
計量経済学モデルは、データ駆動型金融機関の支柱です。経済現象を統計的手法でモデル化することを可能にし、より良い情報に基づく意思決定に導きます。
ロンドンに本社を置くアクティブ投資運用会社Man Groupは、コックス・ロス・ルービンシュタインなどのオプション価格モデルを利用して、毎日何百万ものオプションを評価しています。Man Groupの定量的研究者は、競争力を得るために、このモデルの性能改善に継続的に取り組んでいます。最近のIPU評価の検索では、見事な結果が得られています。
「オプション価格の設定は、Man Groupにとって重要な作業負荷で、計算量が多いです。これをIPUでテストする場合、コックス・ロス・ルービンシュタイン手法がやはりよいベンチマークになります。Graphcoreと共同で実施した最近の調査では、IPUの超並列性が実証されており、CPUよりも最大21倍速くオプション価格を設定できます。」とMan GroupのAlpha Technologyでシニアエンジニアを務めるBalazs Domonkos氏は話しています。
CPUには、簡単にベクトル化できない計量経済学の作業負荷を処理する柔軟性があるため、多くの金融機関で、GPUよりも選択されているハードウェアになっています。IPUは、これらよりも優れています。CPUと同じMIMDの柔軟性を提供することにより、この作業負荷を高速化できると同時に、はるかに高いフロップレートと処理速度を提供するためです。このカテゴリに当てはまる、ベクトル化が難しい作業負荷3種類は、以下のとおりです。
条件付き終了作業負荷。 この作業負荷には、条件が満たされるまで、または入力によって決定される特定の反復回数が完了するまで、ループすることが含まれています。バッチ処理を使用する場合、バッチが完了したと見なされる前に、すべてのサンプルが完了する必要があります。例としては、オートコールイベントが発生した場合に終了できる、オートコール可能オプション価格の設定モデルです。
シーケンシャル作業負荷。 これらには、反復的、ループベース、再帰的な作業が含まれます。何度も実行する必要のないシーケンシャル作業負荷の場合、現在の操作の出力が次の操作への入力として必要になるため、ベクトル化することはできません。例としては、ハミルトニアンダイナミクスを反復的にシミュレーションする、ハミルトニアンモンテカルロです。
入力依存ルーティング作業負荷。 木ベースのモデルおよび条件文(if文)を使用する、他の形式のモデルです。バッチの各要素で実行される操作が異なる場合、この作業負荷をベクトル化するのは難しい可能性があります。深さが変化する決定木(ディシジョン・ツリー)は、その典型的な例です。
このブログの投稿では、コックス・ロス・ルービンシュタイン(CRR)モデルと呼ばれるアルゴリズムを見ていきます。CRRモデルは、その柔軟性により、アメリカン・オプションの保有者がいつでもオプションを行使する権利などの幅広い条件を処理できるため、オプション価格設定の一般的なアルゴリズムになっています。CRRモデルの仕組み、ベクトル化に伴う複雑な問題、IPUでの本番環境での大規模な実装方法について説明します。
コックス・ロス・ルービンシュタイン(CRR)モデルは、評価日と有効期限の間のシミュレーションされたタイムステップ(n)の離散数にわたって資産の価格がどのように変化するかを考慮して、オプション価格を設定します。シミュレーションされたタイムステップ数が多いほど、価格設定はより正確になります。
モデルには2つのフェーズがあります。フォワードパスとして知られるフェーズ1では、原資産の価格が現在のスポット価格S0からシミュレーションされた各タイムステップで、特定の係数(uまたはd)分増減すると仮定して、価格木が生成されます(図1参照)。資産が増減する係数は、資産のボラティリティとシミュレーションされたタイムステップのサイズの関数として計算されます。
バックワードパスとして知られるフェーズ2では、オプションの価値は、価格のツリーをさかのぼって反復的に計算されます。各タイムステップで、前の時点でのオプションの価値は、その原資産が増減した確率を考慮して計算されます。 これは二項値として知られています。
二項パラメータpは、特定のシミュレーションされた時点で価格が上昇する確率を表します。 pは、二項分布が、測定されたボラティリティと想定される割引率で資産のブラウン運動をシミュレーションするように設定されます。
ヨーロピアン・オプションに実装された場合と、アメリカン・オプションに実装された場合とで、アルゴリズムのバックワードパスに違いがあるので、注意が必要です。この違いは、いつでもオプションを行使するアメリカン・オプション保有者の能力を反映する条件を実装することによる、CRRアルゴリズムの柔軟性に基づいています。
CRRアルゴリズムの力は、任意のタイムステップで条件を追加できるユーザーの能力にあります。アメリカン・オプション価格の設定では、オプションの価値が、オプションをすぐに行使することによって得られる価値を下回ることができないという条件が追加されます。
この条件にもかかわらず、木の高さ全体とオプションのバッチの両方で、CRRアルゴリズムをベクトル化することができます。このような実装は、Googleのtf-quant finance library tf-quant-finance/crr_binomial_treeで見ることができます。作者は、アメリカとヨーロッパのオプションの混合バッチ全体でアルゴリズムをベクトル化しています。つまり、バッチ内の各入力がアメリカン・オプションか、ヨーロピアン・オプションかにかかわらず、同じ操作を実行する必要があります。
ヨーロピアン・オプションでは、オプションをすぐに行使することでより高いリターンを達成できるかを計算する必要がないため、アメリカン・オプションよりも処理に必要な操作が少ないです。ただし、この形式のベクトル化では、アメリカとヨーロッパのオプション価格の設定に同じ操作を実行する必要があるため、スループットは2つの間で等しくなります。下記の図1をご覧ください。
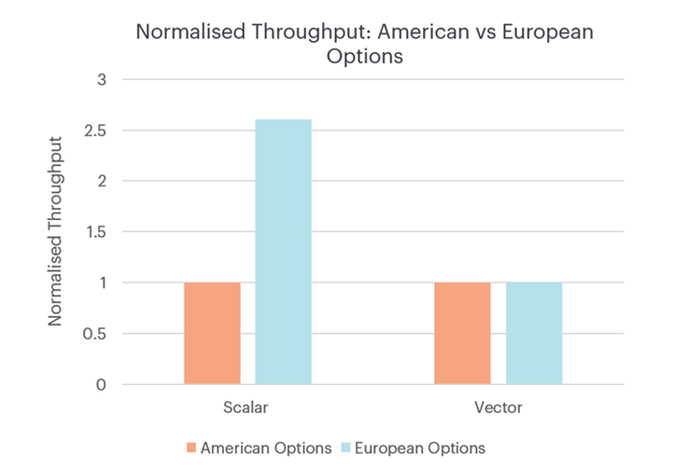
スカラー作業負荷として実装した場合、ヨーロピアン・オプション(青)の価格設定は、アメリカン・オプション(オレンジ)の価格設定よりもはるかに速い。各ケースのスループットは、アメリカン・オプションのスループットに対して正規化。[出典:Graphcoreによるベンチマーク]
これは、コックス・ロス・ルービンシュタインでは、コードの2つのコピー(1つはヨーロピアン・オプション用、もう1つはアメリカン・オプション用)を維持することで比較的簡単に修正され、「if」文が削除されます。とはいえ、コックス・ロス・ルービンシュタインおよびその他の計量経済学モデルのバリエーションになると、修正はそれほど単純ではありません。
ベクトル化された実装よりも、スカラーを使うもう1つの理由は、データの局所性の強制です。ベクトル化された操作でバッチを処理する場合、後続の操作に備えて、データが演算コアとキャッシュの間で交換される可能性があります。コア/スレッド間に相互依存関係がないため、これはスカラー実装では回避できる可能性があります。
CPUやGraphcore IPUなどのMIMDプロセッサには、SIMDプロセッサよりも柔軟性があります。IPUを使用すると、スレッドは、他のスレッドが何を実行しているかにかかわらず、任意の命令を実行できますが、SIMDプロセッサでは、各スレッドが同じ命令を実行する必要があるため、ベクトル化が必要です。
入力依存ルーティングに対応することは、IPUプロセッサでのスカラー操作では簡単です。サンプルのバッチを演算する代わりに、各サンプルは単一のスレッドに分散され、そのサンプルに必要な演算パスを自由に実行できます。つまり、サンプルが収束した場合、処理は停止し、スレッドは制御プログラムに戻されます。そのサンプルのプロパティが原因で、プログラムがコードの特定のセクション(if文)の実行を必要としない場合、プログラムは自由にスキップします。このきめ細かい制御は、バッチ処理では不可能です。
大量のオプション価格を設定する場合も、ハードウェアをワーカーのプールとして扱い、独立した処理のために各ワーカーにオプションを配布することにより、IPUプログラミングモデルで簡単に解決できます。ワーカーが処理を完了すると、制御プログラムに戻り、別のオプションを使用して再度ディスパッチできます。この処理は、CPUの場合と同様に、IPUでも機能します。
CPUとは対照的に、IPUは超並列MIMDチップです。1,472のタイルと8,832の並列スレッドを備え、他のすべてのスレッドから独立して動作できます。つまり、CPUと同様、高性能を実現するためにベクトル化されたプログラムに依存する必要がなく、また、現在利用可能なサーバーグレードのCPUよりも1~2桁多いコアを備えています。
単一のオプションを単一のプロセッサスレッドにマッピングすることで(IPUにはIPUタイルごとに6つのスレッドがあります)、単一のIPUで、並列で、8832のオプションの価格を設定できます。以下で、これを24コア(2xハイパースレッディングで48スレッド)の標準サーバーグレードCPUと比較します。並列で、48のオプションを価格設定します。単一のMK2 IPUと単一のCPU(Intel Xeon Platinum 8168)のスループットの比較は、図2能登通りです。
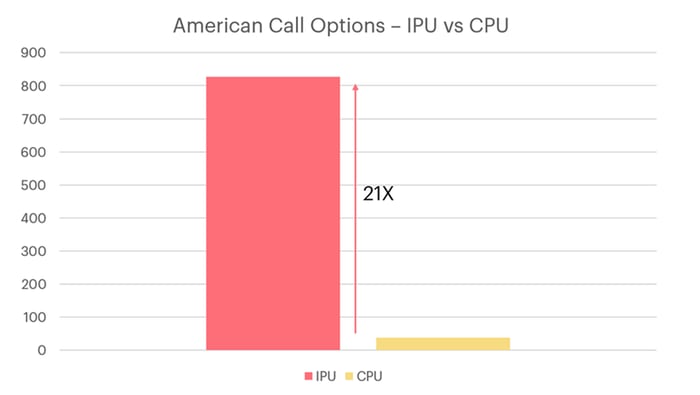
IPUは、CRRアルゴリズムを使用してアメリカン・オプション価格を設定する場合、サーバーグレードのCPUと比較して最大21倍のスループットを提供。[出典:Graphcoreによるベンチマーク]
CRRアルゴリズムがIPUでしっかりと実行されるのは、IPUによる並列処理ばかりが要因になっているわけではありません。CPUは、価格の決定木をオフチップDRAMに格納します。これには、約10GB/秒の読み取り/書き込み速度でアクセスできますが、メモリ階層を使用することで少し向上できます。ですが、IPUは、価格木全体を900MBのプロセッサ内メモリに明示的に格納します。このメモリには、47TB/秒の読み取り/書き込み速度でアクセスできます。
CRRアルゴリズムは、入力依存ルーティングを使用する作業負荷の例であり、この作業負荷の一般的なベクトル化には、可能な限り長い演算パスの速度で実行するという欠点があることを示しました。
CPUには、簡単にベクトル化できない作業負荷を処理する柔軟性があるため、多くの金融機関で選択されているハードウェアになっています。しかしながら、Graphcore IPUは、CPUと同じMIMDの柔軟性を提供することにより、この種の作業負荷を高速化できると同時に、はるかに高いフロップレートと、それゆえの処理速度を提供します。
Sign up for Graphcore updates:
Apr 28, 2025 \ Research, Scientific Research, LLM
Mar 06, 2025 \ Research, Large models, LLM
Feb 04, 2025 \ AI, Research, LLM
下のボックスでサインアップして最新のニュースとアップデートをご覧ください。
Sign up below to get the latest news and updates:

