BERT 패킹: 자연어 처리를 위한 학습 속도를 2배로 향상

새로운 패킹 알고리즘을 사용한 결과, BERT-Large를 학습하는 동안 자연어 처리 속도를 2배 이상 높였습니다. 당사의 새로운 패킹 기술은 패딩을 제거하여 훨씬 더 효율적인 계산을 가능하게 합니다.

비대칭 길이 분포를 가진 다른 모델과 유전체학 및 단백질 접힘 모델에도 이러한 기술을 적용하여 다른 산업 및 응용 분야에서 훨씬 더 광범위한 효과를 얻을 수 있을 것으로 예상됩니다.

새로 발표한 논문에서는 패킹된 시퀀스에 적용된 BERT 알고리즘과 그래프코어의 고효율 NNLSHP(Non-Negative Least Squares Histogram-Packing, 비음수 최소자승 히스토그램 패킹)를 소개한 바 있습니다.

시퀀스 패딩으로 인한 NLP(자연어 처리)에서의 컴퓨팅 낭비

최근 MLPerf^TM에 대한 벤치마크 제출 작업을 하면서 BERT 학습을 최적화하는 새로운 방법을 조사하기 시작했습니다. 목표는 실제 응용 시 쉽게 채택할 수 있는 유용한 최적화 방법을 개발하는 것이었습니다. BERT는 업계에서 많은 고객이 널리 사용하기 때문에 이러한 최적화에 집중해야 하는 모델 중 하나로 자연스럽게 선정되었습니다.

우리는 Wikipedia 데이터셋을 사용하는 자체 BERT-Large 학습 애플리케이션에서 데이터셋에 있는 토큰의 50%가 패딩되어 많은 컴퓨팅 낭비를 발생시킨다는 사실을 알게 되었습니다. 

시퀀스를 모두 동일한 길이로 정렬하는 패딩 시퀀스는 GPU에서 사용되는 일반적인 접근 방식이지만, 다른 접근 방식을 시도해 볼 가치가 있다고 생각했습니다. 

시퀀스는 다음 두 가지 이유로 길이가 크게 변동합니다.

1. 기본 Wikipedia 데이터에서 문서 길이의 변동이 크게 나타납니다.
2. BERT 전처리 자체는 학습 시퀀스를 생성하기 위해 결합되는 추출 문서들의 크기를 무작위로 줄입니다.

길이를 최대 길이인 512로 채우면 전체 토큰의 50%가 패딩 토큰이 됩니다. 패딩의 50%를 실제 데이터로 교체하면 동일한 컴퓨팅 조치로 50% 더 많은 데이터를 처리할 수 있으므로 최적의 조건에서 속도가 2배 빨라지는 것과 마찬가지입니다.

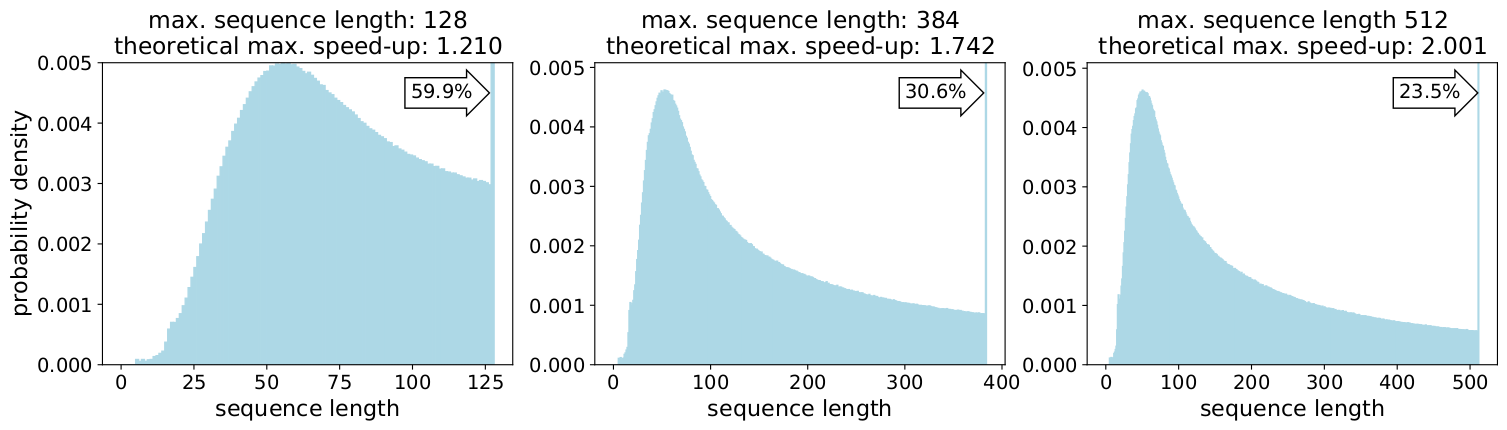
Wikipedia에만 해당되나요? 그렇지 않습니다. 

그렇다면 언어별로 결과가 다른가요? 그렇지 않습니다. 

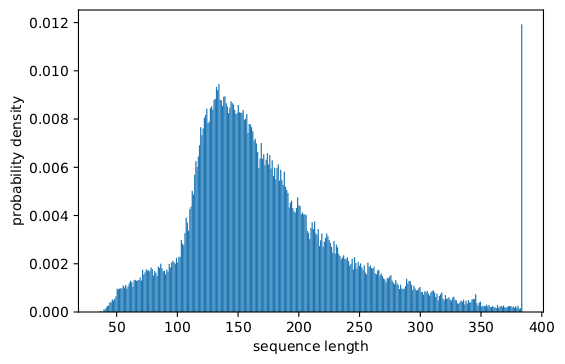
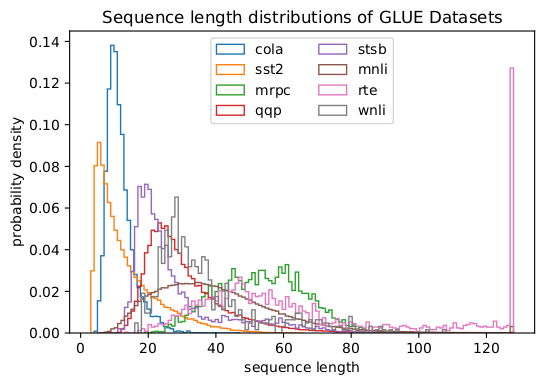
사실 비대칭 길이 분포는 언어, 유전체학 및 단백질 접힘 등 모든 곳에서 발견됩니다. 그림 2와 3은 SQuAD 1.1 데이터셋과 GLUE 데이터셋의 분포를 보여줍니다.

컴퓨팅 낭비를 피하면서 상이한 길이를 처리하려면 어떻게 해야 할까요? 

현재 접근 방식에서는 서로 다른 길이에 서로 다른 컴퓨팅 커널을 사용하거나, 엔지니어가 프로그래밍 방식으로 패딩을 제거한 다음 각각의 어텐션 블록 및 손실 계산에 대해 반복적으로 다시 추가해야 합니다. 코드를 부풀리고 더 복잡하게 만들어서 컴퓨팅을 줄이는 방안은 적절하지 않은 것으로 판단했기 때문에 더 나은 방법을 모색했습니다. 최대 길이의 팩에 여러 시퀀스를 함께 넣고 처리할 수 있을지 연구해 본 결과, 가능한 것으로 밝혀졌습니다. 

이 접근 방식에는 세 가지 핵심 요소가 필요합니다.

1. 남은 패딩을 최소한으로 줄이기 위해 조합할 샘플을 결정하는 효율적인 알고리즘
2. 시퀀스 대신 팩을 처리하도록 BERT 모델 조정
3. 하이퍼 매개변수 조정

패킹

처음에는 Wikipedia와 같은 대규모 데이터셋을 효율적으로 패킹하기가 어려워 보였습니다. 이 문제는 일반적으로 빈 패킹(bin-packing) 문제로도 알려져 있습니다. 패킹이 3개 이하의 시퀀스로 제한되는 경우에도 결과적으로 효율적인 알고리즘 솔루션이 결여된 상태의 강력한 NP-완전 문제가 발생합니다. 기존의 휴리스틱 패킹 알고리즘은 최소 \(O(n log(n))\)의 복잡성을 가지기 때문에 바람직하지 않았습니다. 여기서 n은 시퀀스 수(Wikipedia의 경우 ~16M)를 의미합니다. 따라서 수백만 개의 시퀀스로 확장되는 접근 방식에 관심을 갖게 되었습니다. 

우리는 두 가지 요령을 통해 복잡성을 크게 줄일 수 있었습니다.

1. 팩의 시퀀스 수를 3개로 제한(첫 번째 솔루션 접근 방식의 경우)
2. 발생하는 각 길이에 대해 하나의 빈이 있는 시퀀스 길이의 히스토그램에서만 시행

최대 시퀀스 길이는 512였습니다. 따라서 히스토그램으로 이동하면 차원과 복잡성이 1,600만 시퀀스에서 512 길이 수치로 감소했습니다. 한 팩에 최대 3개의 시퀀스를 허용한 결과, 허용되는 길이 조합 수를 22,000으로 줄일 수 있었습니다. 여기에는 시퀀스가 팩에서 길이별로 정렬되도록 요구하는 요령이 이미 포함되어 있었습니다. 4개의 시퀀스를 시도하면 어떨까요? 그 결과 조합 수가 22,000에서 940,000으로 증가했으며, 이는 첫 번째 모델링 접근 방식에 있어 너무 많은 결과였습니다. 또한 뎁스 3은 이미 상당히 높은 패킹 효율을 달성했습니다.

원래 한 팩에 3개가 넘는 시퀀스를 사용하면 컴퓨팅 오버헤드가 증가하고 학습 중 컨버전스 행동에 영향을 미칠 것이라고 생각했습니다. 그러나 더 빠른 실시간 패킹이 필요한 추론과 같은 분야를 지원하기 위해 고효율 NNLSHP 알고리즘을 개발했습니다.

NNLSHP(Non-Negative Least Squares Histogram-Packing, 비음수 최소자승 히스토그램-패킹)

빈 패킹은 수학적 최적화 문제로 표현되는 경우가 많습니다. 그러나 1,600만 개 이상의 시퀀스에서는 실용적이지 않으며, 문제 변수만으로도 대부분의 시스템 메모리를 초과합니다. 히스토그램 기반 접근 방식용 수학적 프로그램은 매우 깔끔합니다. 우리는 단순화를 위해 히스토그램 벡터 \(b\)를 사용한 최소 자승법(\(Ax=b\))을 사용하기로 결정했습니다. 전략 벡터 x가 음이 아닌 것을 요구하고 약간의 패딩을 허용하도록 가중치를 추가하여 이를 확장했습니다.

까다로운 부분은 전략 매트릭스였습니다. 각 열의 최대 합은 3이고 원하는 총 길이와 정확히 일치하도록 함께 패킹되는 시퀀스를 인코딩하며, 당사의 경우에는 512입니다. 행은 전체 길이에 도달할 수 있는 각 잠재적 조합을 인코딩합니다. 전략 벡터 \(x\)는 이 경우에 적합한 방법으로, 20,000개의 조합 중 임의의 조합을 선택하는 빈도를 나타냅니다. 결과적으로는 흥미롭게도 마지막에 약 600개의 조합만 선택되었습니다. 정확한 솔루션을 얻으려면 x의 전략 수는 양의 정수여야 하지만, 음이 아닌 \(x\)만 있는 근사 반올림 솔루션이면 충분하다는 것을 깨달았습니다. 근사 솔루션의 경우 간단하고 즉각적으로 사용할 수 있는 솔버를 통해 30초 이내에 결과를 얻을 수 있습니다.

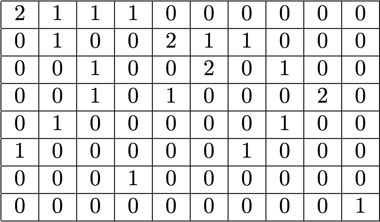
결국, 우리는 전략이 할당되지 않은 샘플을 수정해야 했지만 그 수는 매우 적었습니다. 또한 각 시퀀스가 잠재적으로 패딩과 함께 패킹되고 패딩에 따라 가중치가 적용되도록 하는 변형 솔버를 개발했습니다. 하지만 시간이 훨씬 더 오래 걸리고 솔루션도 크게 나을 것이 없었습니다.

SPFHP(Shortest-Pack-First Histogram Packing, 최단 팩 첫 히스토그램 패킹)

NNLSHP는 충분한 패킹 접근 방식을 제공했습니다. 그러나 이론적으로 더 빠른 온라인 접근 방식을 얻고 3개의 시퀀스만 함께 배치하는 제한을 없앨 수 있는지 궁금했습니다.

따라서 우리는 기존 패킹 알고리즘에서 약간의 아이디어를 얻기는 했지만 여전히 히스토그램에 중점을 두었습니다. 

첫 번째 알고리즘인 SPFHP에는 네 가지 요소가 있습니다.

1. 가장 긴 시퀀스에서 가장 짧은 시퀀스까지 히스토그램의 수를 계산합니다.
2. 현재 시퀀스 길이가 팩에 맞지 않으면 새 팩 세트를 시작합니다.
3. 길이가 맞는 팩이 여러 개일 경우 시퀀스 길이의 합이 가장 짧은 팩을 선택하고 각각 수를 수정합니다.
4. 나머지 수에 대해 길이가 맞는지 다시 확인합니다.

이 접근 방식은 구현하기 가장 간단했고 0.02초밖에 걸리지 않았습니다.

다른 방법은 더 완벽하게 맞는 항목을 찾기 위해 가장 짧은 수와 분할 수 대신 시퀀스 길이의 가장 큰 합을 취하는 것이었습니다. 전반적으로 효율성은 크게 달라지지 않았지만 코드 복잡성이 많이 증가했습니다.

Wikipedia, SQuAD 1.1, GLUE 패킹 결과

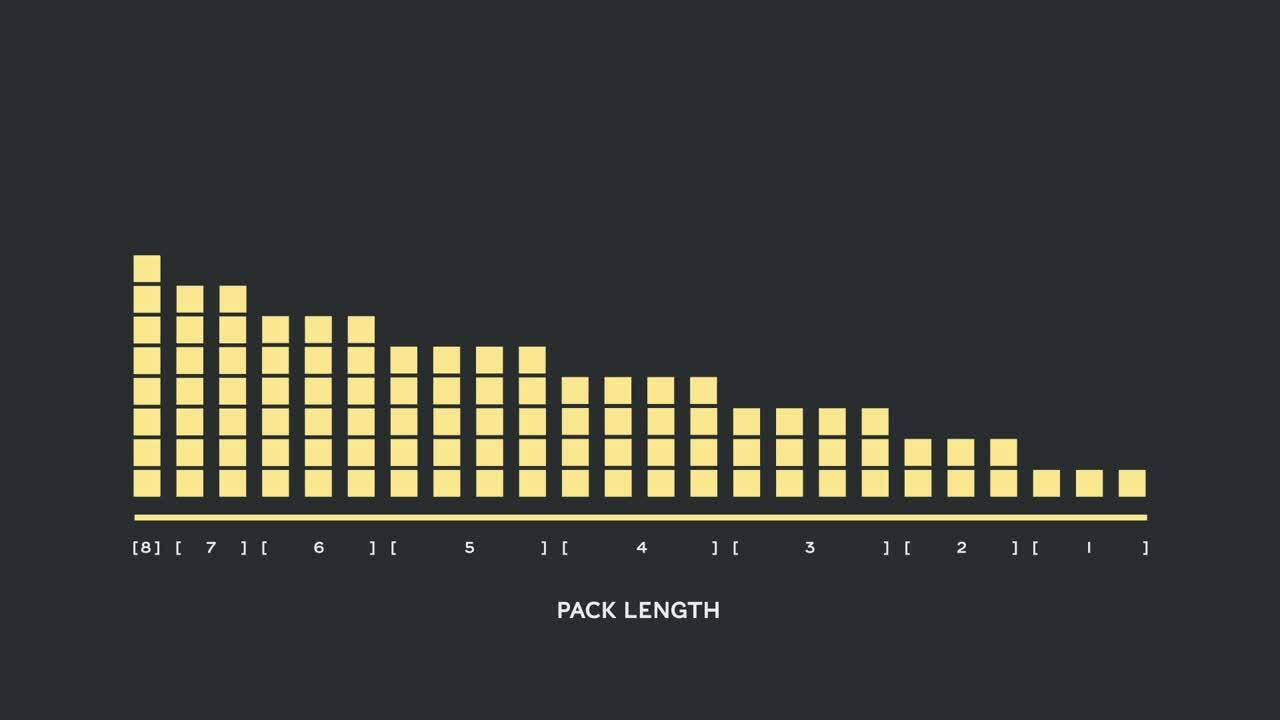
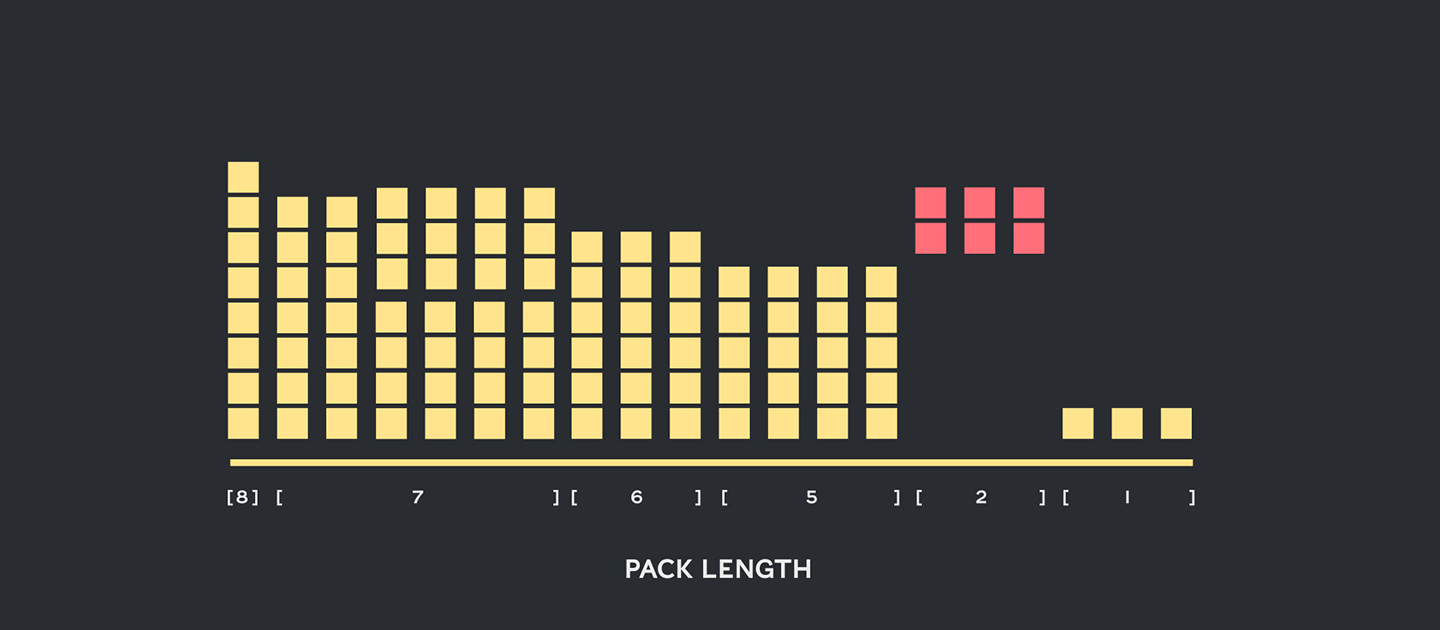
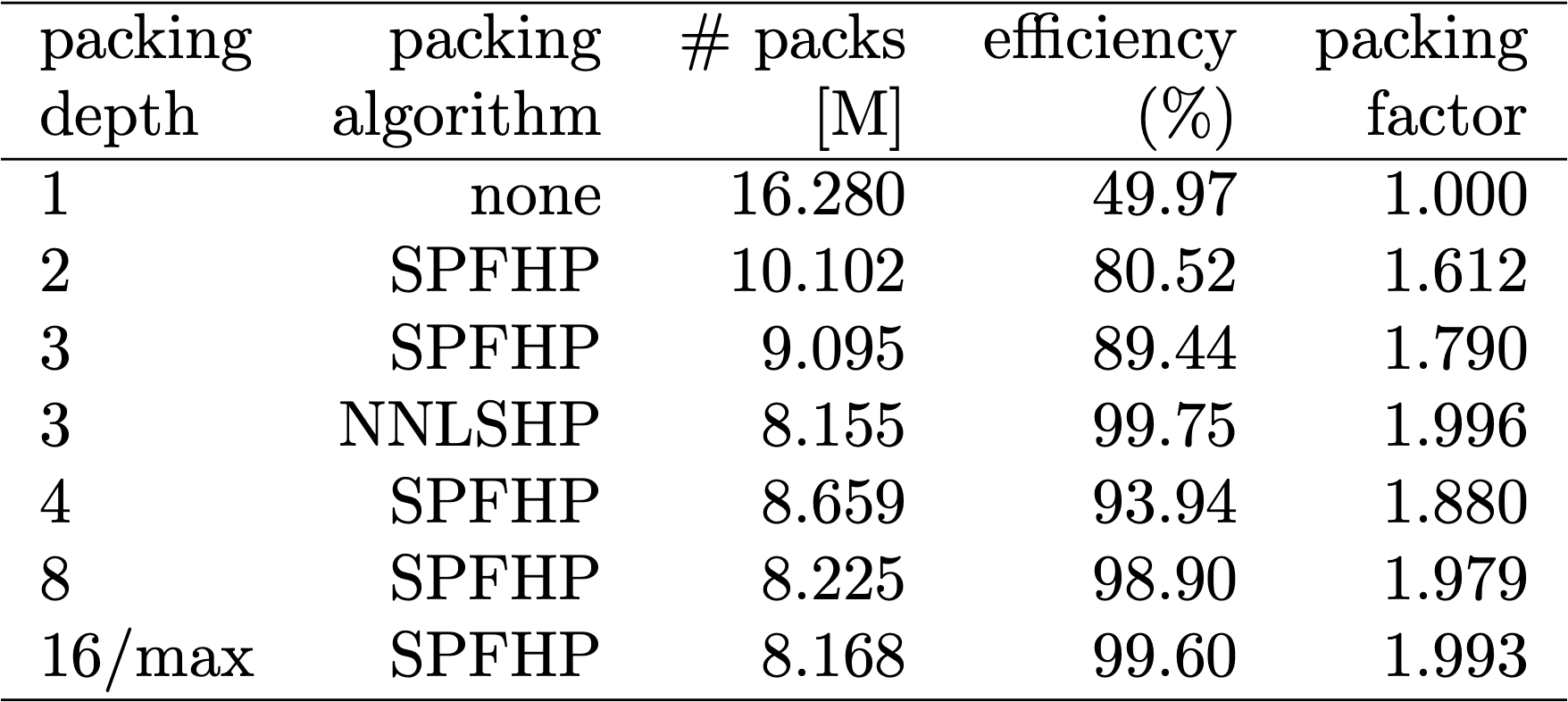
표 1, 2, 3은 제시된 두 알고리즘의 패킹 결과를 보여줍니다. 패킹 뎁스는 패킹된 시퀀스의 최대 수를 나타냅니다. 패킹 뎁스 1은 기준 BERT 구현입니다. 최대 발생 패킹 뎁스는 제한이 설정되지 않은 경우 "최대"로 추가 표시됩니다. 팩 수는 새로 패킹된 데이터셋의 길이를 나타냅니다. 효율성은 패킹된 데이터셋에서 실제 토큰이 차지하는 비율입니다. 패킹 인수는 패킹 뎁스 1에 비해 결과적으로 초래된 잠재적인 속도 향상을 나타냅니다.

네 가지 주요 관찰 사항이 있었습니다.

1. 분포가 더 편향될수록 패킹의 이점이 높아집니다.
2. 모든 데이터셋은 패킹을 통해 이점을 얻습니다. 일부 데이터셋의 경우 그 효과는 2배 이상입니다.
3. SPFHP는 패킹 뎁스가 제한되지 않을 때 더 효율적입니다.
4. 최대 3개의 패킹된 시퀀스의 경우 NNLSHP가 더 복잡할수록 더 효율적입니다(99.75 대 89.44).

표 1: Wikipedia에대해 제시된 패킹 알고리즘(SPFHP 및 NNLSHP)의 주요 성능 결과

표 2: SQUaD 1.1 BERT 사전 학습을 위해 제시된 패킹 알고리즘의 성능 결과

표 3: GLUE 데이터세트에 대해 제시된 패킹 알고리즘의 성능 결과. 패킹 뎁스를 제한하지 않은 기준 및 SPFHP 패킹 결과만 표시되었습니다.

BERT 처리 조정

BERT 아키텍처에서 흥미로운 점은 대부분의 처리가 토큰 수준에서 발생하므로 패킹을 방해하지 않는다는 것입니다. 조정이 필요한 4가지 구성 요소는 어텐션 마스크, MLM 손실, NSP 손실 및 정확도입니다.

서로 다른 수의 시퀀스를 처리하는 4가지 접근 방식의 핵심은 벡터화와 연결 가능한 최대 수의 시퀀스를 사용하는 것이었습니다. 어텐션에 관해서는 패딩을 다루는 마스크가 이미 있었습니다. 이를 여러 시퀀스로 확장하는 것은 다음 TensorFlow 유사 코드에서 볼 수 있듯이 간단했습니다. 중요한 개념은 어텐션이 별도의 시퀀스로 제한되고 그 이상으로 확장될 수 없음을 확인했다는 것입니다.

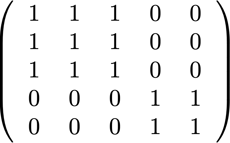
손실 계산을 위해 원칙적으로 시퀀스들을 언패킹하고 별도의 손실을 계산하여 결과적으로 시퀀스(팩 대신)에 대한 손실의 평균을 얻습니다. 

MLM 손실의 경우 코드는 다음과 같습니다.

NSP 손실과 정확도에 있어서 원리는 동일합니다. 공개 예에서 자체 PopART 프레임워크를 사용하여 해당 코드를 찾을 수 있습니다.

Wikipedia 오버헤드 및 속도 향상 추정치

BERT를 수정하면서 두 가지 의문이 생겼습니다.

1. 얼마나 많은 오버헤드가 발생하는가?
2. 오버헤드는 팩에 함께 포함되는 최대 시퀀스 수에 따라 얼마나 달라지는가?

BERT에서 데이터 준비는 번거로울 수 있으므로 손쉬운 방법을 사용하고 여러 다른 패킹 뎁스에 대한 코드를 컴파일하여 각각의 (측정된) 주기를 비교했습니다. 결과는 표 4에 나와 있습니다. 오버헤드는 패킹을 가능하게 하는 모델 변경(예: 어텐션을 위한 마스킹 방식 및 변경된 손실 계산)으로 인한 처리량 감소 비율을 나타냅니다. 속도 향상은 패킹(패킹 인수)으로 인한 속도 향상과 오버헤드로 인한 처리량 감소가 조합된 결과입니다.

표 4: Wikipedia에 대해 제시된 패킹 알고리즘(SPFHP 및 NNLSHP)의 예상 속도 향상 비교

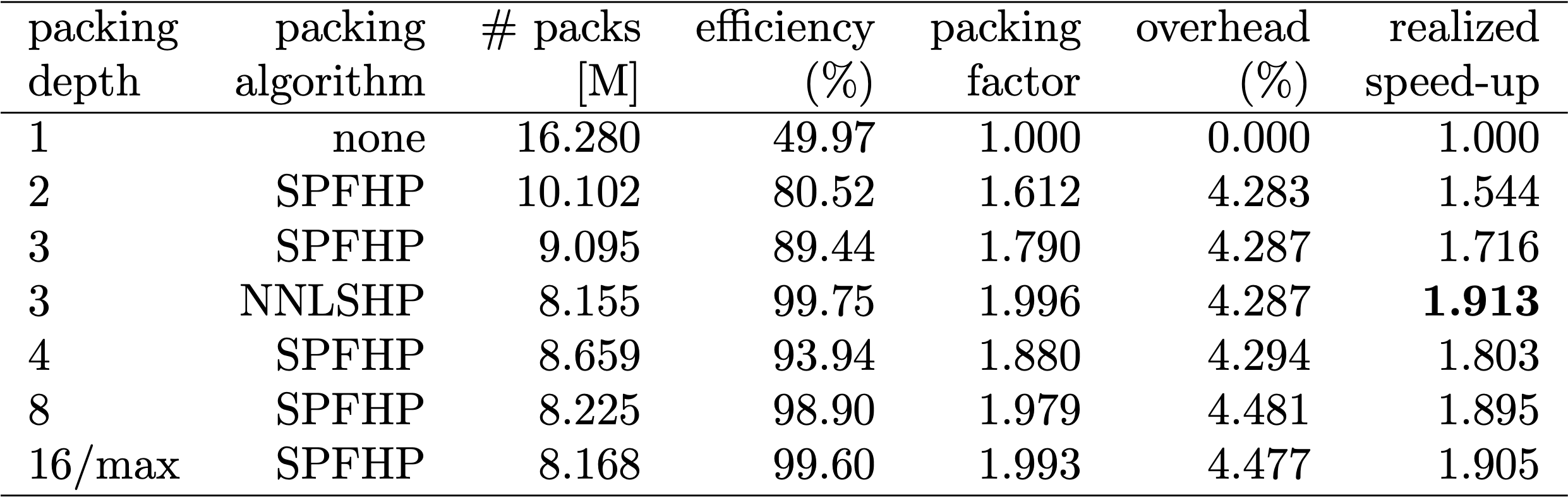
벡터화 기술을 사용한 결과로 오버헤드가 매우 작으며 많은 시퀀스를 함께 묶는 것에 대한 불이익도 없습니다.

하이퍼 매개변수 조정

패킹을 통해 유효 배치 크기(평균)를 두 배로 늘리고 있으며, 따라서 학습 하이퍼 매개변수를 조정해야 합니다. 간단한 요령은 학습 전과 동일한 유효 평균 배치 크기를 유지하기 위해 그래디언트 축적 수를 절반으로 줄이는 것입니다. 사전 학습된 체크포인트와 함께 벤치마크 설정을 사용하여 정확도 곡선이 완벽하게 일치함을 확인할 수 있습니다.

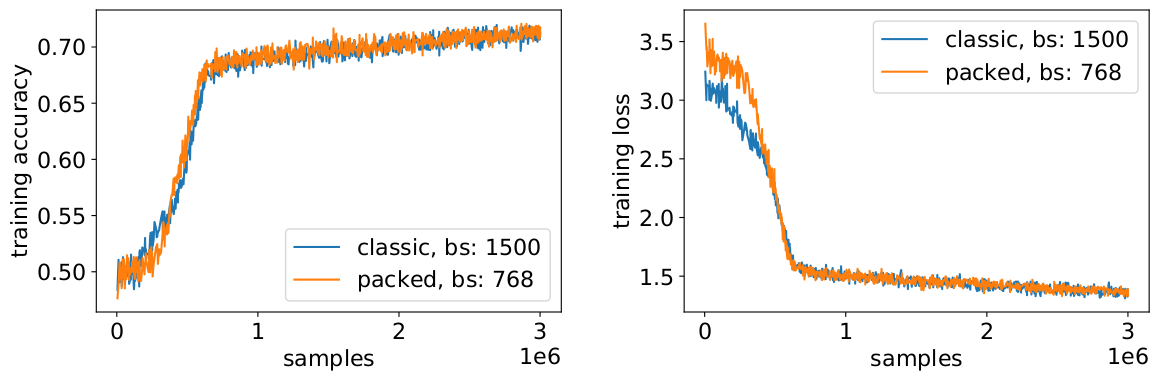
정확도 일치: MLM 학습 손실은 처음에는 약간 다를 수 있지만 그 차이를 빠르게 따라잡습니다. 이 초기 차이는 이전 학습에서 짧은 시퀀스로 편향되었을 수 있는 어텐션 레이어의 미세한 조정 때문일 수 있습니다.

속도 저하를 피하기 위해 때로는 원래 배치 크기를 동일하게 유지하고 하이퍼 매개변수를 증가된 유효 배치 크기(2배)로 조정하는 것이 도움이 됩니다. 고려해야 할 주요 하이퍼 매개변수는 베타 매개변수와 학습률입니다. 한 가지 일반적인 접근 방식은 배치 크기를 두 배로 늘리는 것인데, 우리의 경우에는 성능이 저하되었습니다. LAMB 옵티마이저의 통계를 보면 베타 매개변수를 패킹 인수의 거듭제곱으로 높이는 것이 모멘텀과 속도를 비슷하게 유지하기 위해 여러 배치를 연속적으로 학습하는 것에 상응함을 증명할 수 있었습니다.

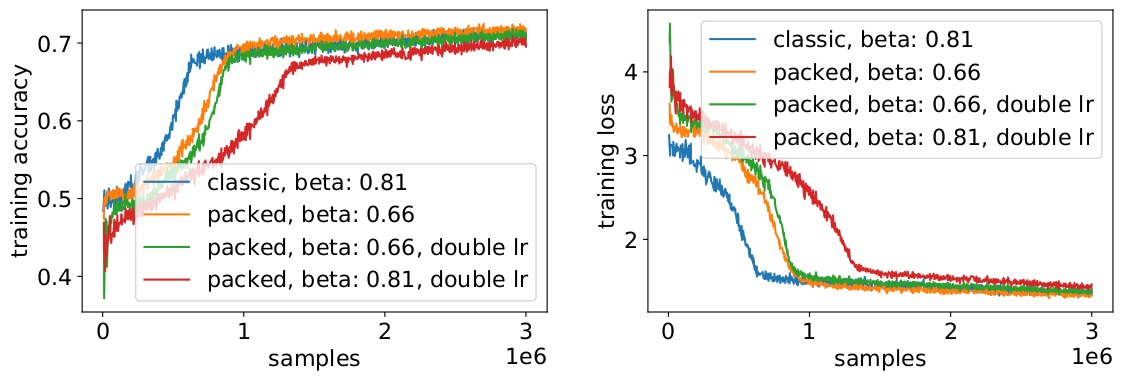
실험 결과, 베타를 2의 거듭제곱으로 취하는 것이 좋은 경험적 방법이라는 것을 알 수 있었습니다. 이 시나리오에서는 배치 크기를 늘리면 일반적으로 목표 정확도에 도달할 때까지 샘플/에포크 측면에서 컨버전스 속도가 감소하기 때문에 곡선들이 일치하지 않을 것으로 예상됩니다.

그러면 실제 시나리오에서 예상한 속도 향상을 실제로 얻을 수 있을까요?

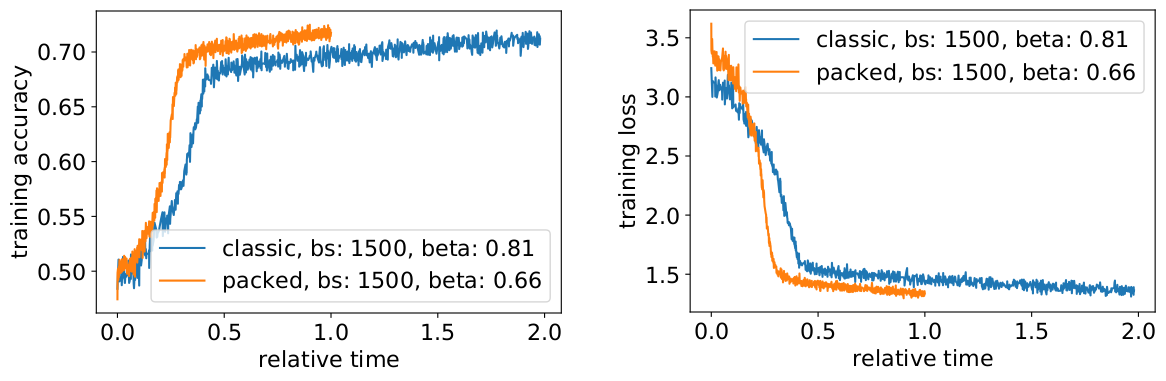
실제로 속도가 향상됩니다! 데이터 전송을 압축했기 때문에 속도가 추가로 향상되었습니다. 

결론

패킹을 통해 컴퓨팅에 드는 노력을 절감하고 환경을 지킬 수 있습니다. 이 기술은 PyTorch 및 TensorFlow를 포함한 모든 프레임워크에서 구현될 수 있습니다. 우리는 확실하게 2배의 속도 향상을 달성했고 그 과정에서 패킹 알고리즘의 기술적 수준을 높였습니다. 

앞으로 더 탐구해볼 만한 다른 응용 분야는 유사한 데이터 분포를 관찰할 수 있는 유전체학 및 단백질 접힘입니다. 비전 트랜스포머는 다양한 크기의 패킹된 이미지를 적용하는 흥미로운 영역이 될 수도 있습니다. 어떤 분야에서 좋은 효과를 얻을 수 있을까요? 의견을 알려주세요!

논문 읽기

GitHub에서 코드에 액세스

감사합니다.

도움을 주신 그래프코어 애플리케이션 엔지니어링 팀의 동료 Sheng Fu와 Mrinal Iyer에게 감사드리며, 귀중한 피드백을 제공해 주신 그래프코어 리서치 팀의 Douglas Orr에게도 감사드립니다.